MI FGSM:集成模型和黑盒攻击方法
本文是NIPS 2017 Adversarial Attacks and Defenses Competition中non-targeted attack和targeted attack赛道的第一名,投稿至CVPR 2018

文章中提到L-BFGS、FGSM、I-FGSM 、自适应查询等。自适应查询算法虽然不用获得损失函数,但是需要大量查询,不实际。经典算法(FGSM、I-FGSM)具有局限性。简单来说就是,FGSM具有弱白盒强黑盒,I-FGSM强白盒弱黑盒。
文章提出了两个生成黑盒对抗性样本的技术——MI-FGSM和Attacking ensemble of models(攻击整体模型)方法。
MI-FGSM 基于动量迭代梯度的方法
早前的基于梯度的方法
基于梯度的一步方法有快速梯度符号方法(FGSM)和快速梯度方法(FGM),两者都在通过最小化损失函数$J(x^,y)$来寻找一个对抗样本$x^$,一般损失函数是交叉熵。
FGSM是使用$L_\infty$范数$|x^*-x|_\infty<\epsilon$,
$$ \begin{align} x^&=x+\epsilon\cdot sign(\nabla_xJ(x,y)) \end{align*} $$
FGM是使用$L_2$范数$|x^-x|_2<\epsilon$,可以看成是FGSM的拓展形式, $$ \begin{align} x^=x+\epsilon\cdot\frac{\nabla_xJ(x,y)}{|\nabla_x(x,y)|_2} \end{align} $$
基于迭代的梯度方法主要是I-FGSM,
$$
\begin{align}
x_0^&=x,\
\alpha &=\frac\epsilon T,\
x^{t+1}&=x_t^+\alpha\cdot sign(\nabla_xJ(x_t^,y))
\end{align*}
$$
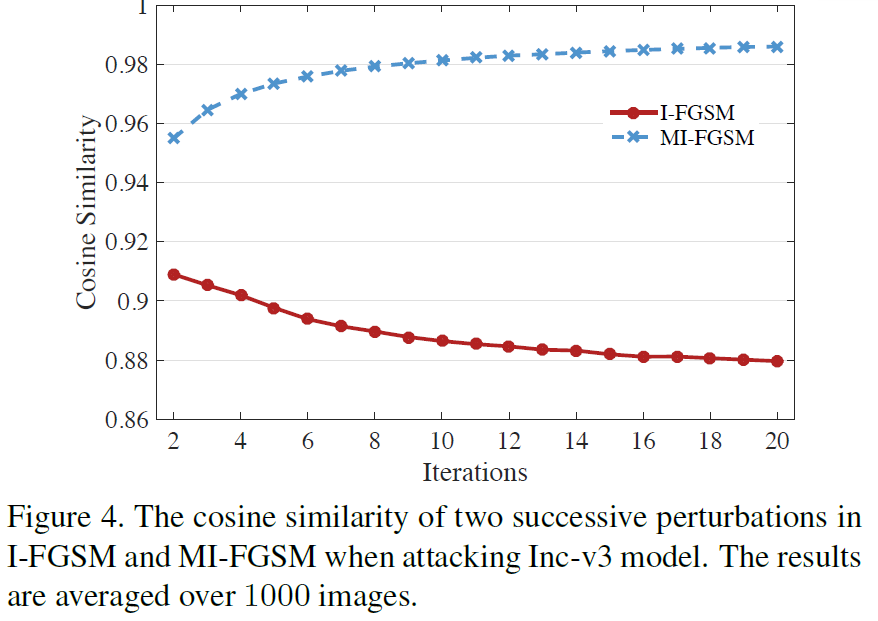
结论:FGSM通过在数据点周围决策边界的线性假设下仅一次将梯度的符号应用于真实示例来生成一个对抗样本。但是,实际上,当失真较大时,线性假设可能不成立,这使得FGSM生成的对抗样本不足于模型,从而限制了其攻击能力。相反,I-FGSM在每次迭代中将对抗样本沿梯度符号的方向贪婪地移动。因此,对抗样本很容易掉入不良的局部最大值并“过度拟合”模型,这不太可能在模型之间转移。
MI-FGSM
以下是MI-FGSM的算法,在(6)式中使用衰减因子$\mu$收集前t次迭代的梯度,可以保留梯度的大致方向,防止陷入不好的局部最优值。每次迭代中使用$L_1$距离(任何距离都是可行的)做归一化。

基于集成模型生成对抗性样本
集成方法已广泛用于研究和竞赛中,以提高性能和鲁棒性。集成的概念也可以应用于对抗性攻击,因为如果一个示例仍然对多个模型具有对抗性,那么它可能会捕获一个固有的方向,该方向总是使这些模型蒙蔽,并且更有可能同时转移到其他模型,从而启用强大的黑盒攻击。
文中使用了将logit激活(logits是softmax的输入值)融合在一起的多个模型。
$$
\begin{align}
l(x)&=\sum_{k=1}^K\omega_kl_k(x) \
J(x,y)&=-label_y\cdot log\left(softmax\left(l\left(x\right)\right)\right)
\end{align}
$$
$l_k(x)$:第$k$个模型的logits
$\omega_k$:权重,$\sum \omega_k =1$
$J(x,y)$:给定标签y和对数$l(x)$的softmax交叉熵损失
$label_y$:y的one-hot编码

结果
单一模型生成的对抗性样本
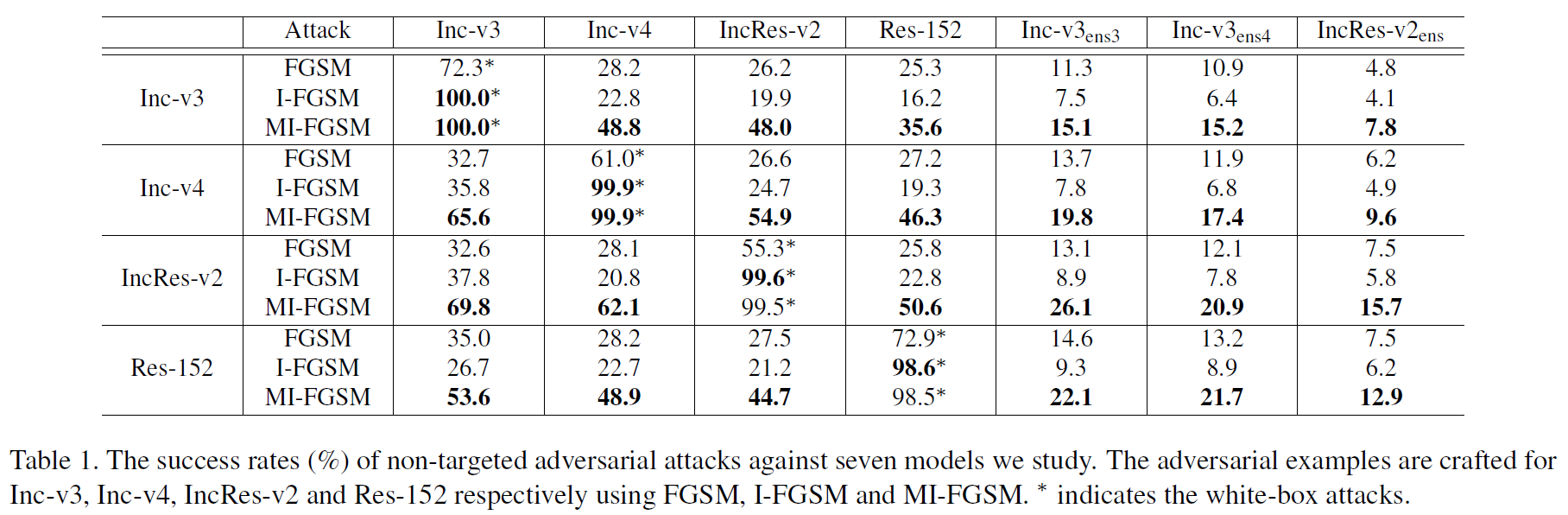
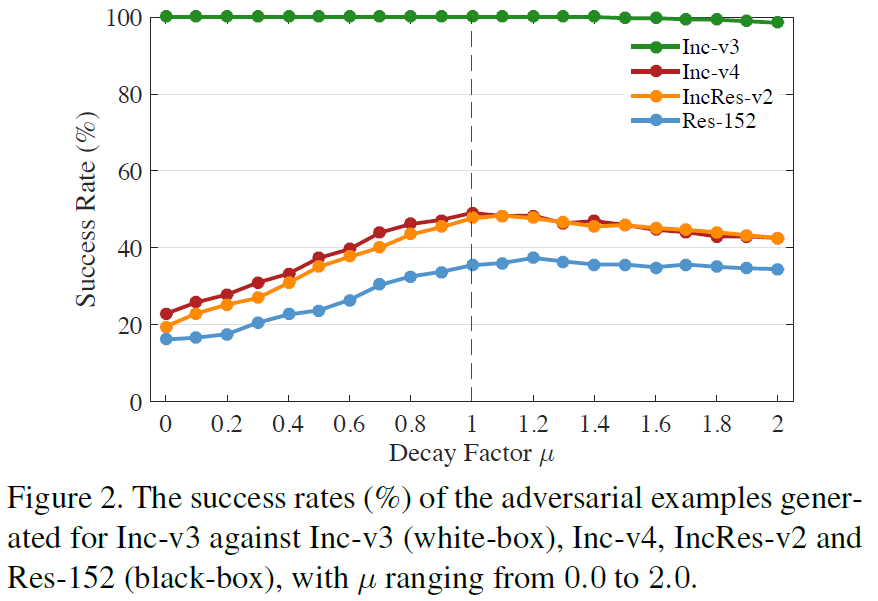
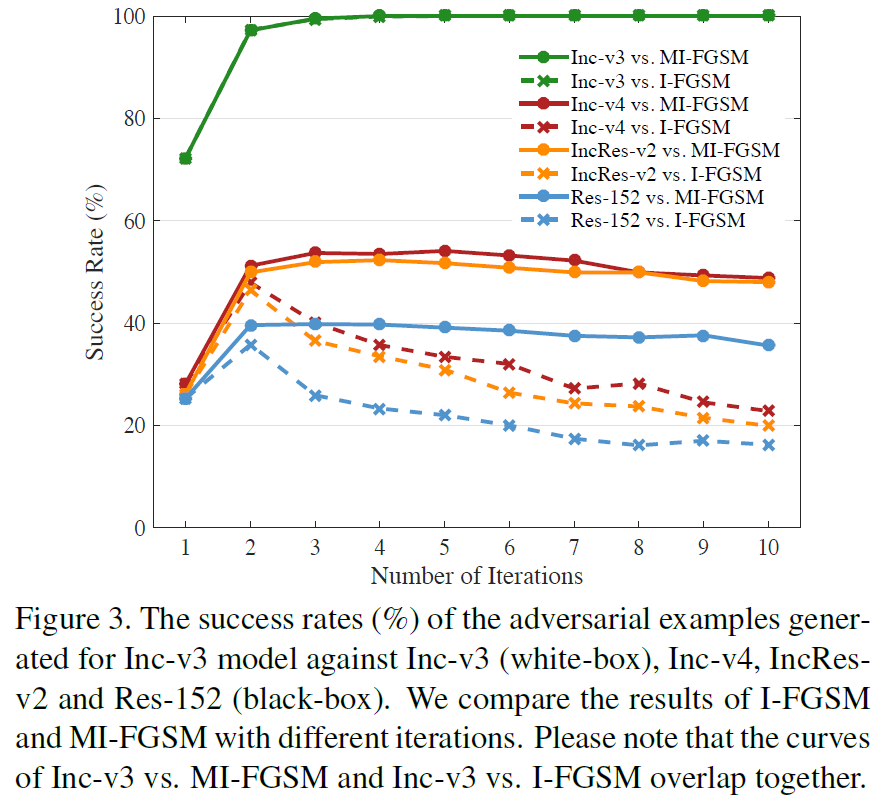
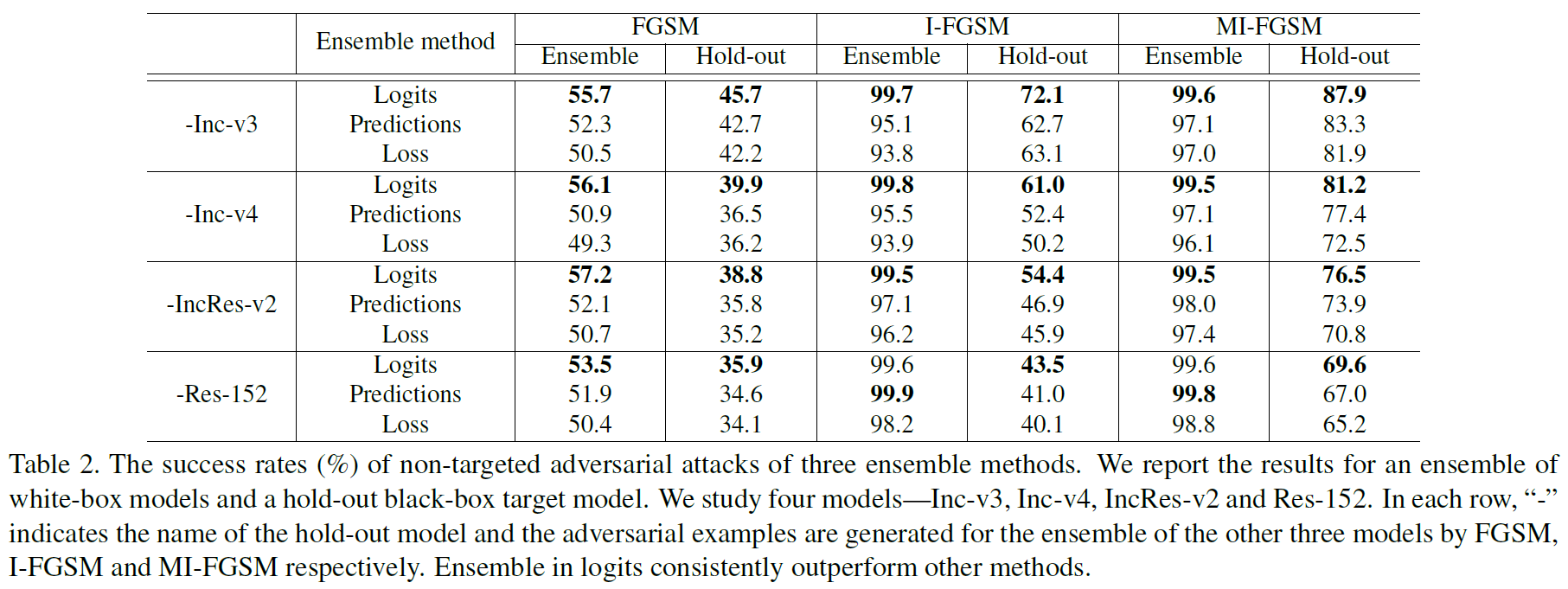
集成模型生成的对抗性样本
集成的实验,一般是三个做集成,留出一个当黑盒,就是hold-out,加-的就是留出的那个model。
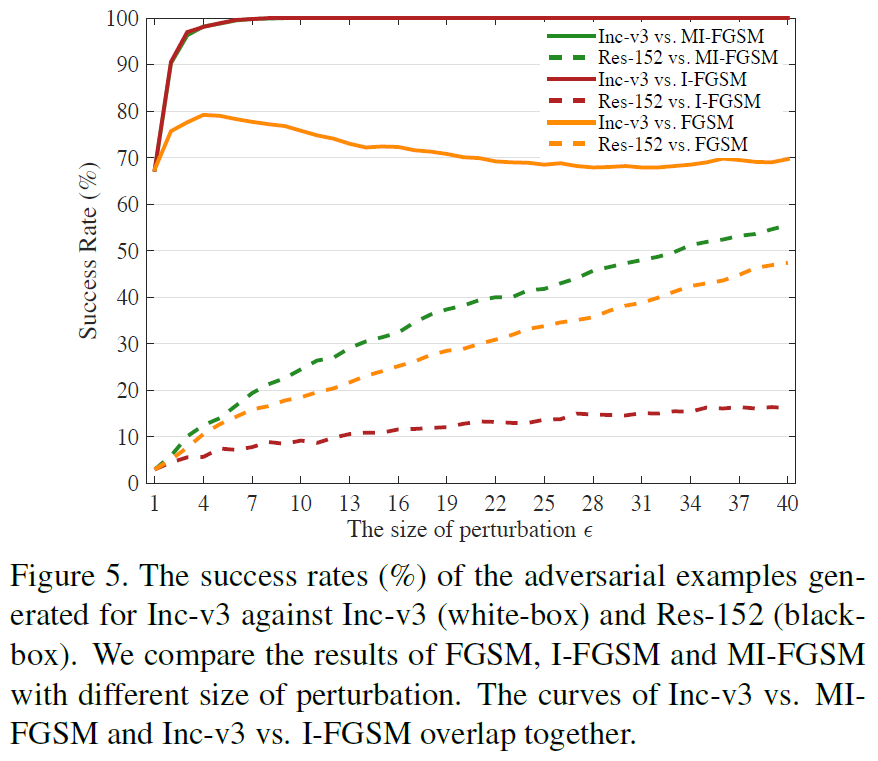
攻击经过对抗训练的模型: