过去认为对抗性样本攻击是由于模型过于非线性化导致的。文章提出的成因恰好相反，认为对抗性样本攻击是由于机器学习模型过于线性化导致的。在文章中阐述了原因，并提出了使用对抗性学习去防御对抗性样本攻击的方法。

image-20201030120717026

Abstract

  • We argue instead that the primary cause of neural networks’ vulnerability to ad- versarial perturbation is their linear nature.

Introduction

  • Szegedy et al. (2014b)1是第一篇正式提出发现对抗性样本攻击的文章
  • In many cases, a wide variety of models with different architectures trained on different subsets of the training data misclassify the same adversarial example. 迁移性
  • This suggests that adversarial examples expose fundamental blind spots in our training algorithms.
  • previous speculative explanations have suggested it is due to extreme nonlinearity of deep neural networks, perhaps combined with insufficient model averaging and insufficient regularization of the purely supervised learning problem.
  • We show that these speculative hypotheses are unnecessary.
    • Linear behavior in high-dimensional spaces is suf- ficient to cause adversarial examples.
  • 这个解释引起了对模型线性化易训练和非线性化防止对抗性攻击之间的权衡考量
  • 主要是Szegedy et al. (2014b)1的工作
    • 提出可靠的对抗性样本生成算法：L-BFGS
    • 生成的对抗性样本无法被人言察觉
    • 使用softmax的回归模型也会被对抗性样本攻击
    • 对抗性训练可以提高抗性
  • DNN models performing well on test datasets are not learning the true underlying concepts that determine the correct output label.

对抗性样本的线形解释

$$ \omega^Tx’=\omega^T(x+\eta)=\omega^Tx+\omega^T\eta $$

  • 在最大化范数的约束下，通过sign()函数来最大化此增量
  • 产生$\eta<\epsilon$可能很小，但是经过线形系统$\omega$之后，它的影响将会增大。假设$\omega$是$n$维的向量，但是每一个维度的平均值是$m$，那么在激活函数输入端，$\eta$将会增长到$mn\eta$。由$\eta$引起的激活函数的变化可以跟随$n$呈线性增长。对于高维问题，我们可以对输入进行许多微小的改变，这些变化加起来就是输出的一个大变化。
  • 线性膨胀 accidental steganography

非线形模型的线性对抗性扰动

  • LSTM、Relu、maxout网络都是有意设计成以非常线性的方式表现的，因为更容易优化。非线性模型（如sigmoid 网络）为了更容易优化，也将大部分时间花在调整为非饱和、更线性的状态。
  • 提出FGSM算法

$$ \eta=\epsilon \times sign(grad_x(J(\theta,x,y))) $$

image-20201030130006571

对抗训练

Szegedy et al. (2014b)1使用对抗性样本和干净样本混合去训练模型来提高其对对抗性样本攻击的抵抗力，这是一种数据增强的方法。作者发现基于FGSM的对抗目标函数训练是一种有效的正则化器 $$ J’(\theta,x,y)=\alpha J(\theta,x,y)+(1-\alpha)J(\theta,x+\eta,y) $$

为什么有大量的对抗性样本

对抗性样本天生具有迁移性。基于一个模型生成的对抗性样本往往可以使其他相同功能但是实现方式不同的模型发生同样的错误错误（识别结果一样）。非线性解释无法解释这一现象。

作者假设神经网络是一些基于相同训练集的线性分类器集合。当在训练子集上进行训练时，此分类器能够学习大约相同的分类权重，因为机器学习算法的泛化能力。基础分类权重（即能够学习大约相同的分类权重）的稳定性反过来又导致对抗样本的稳定性。

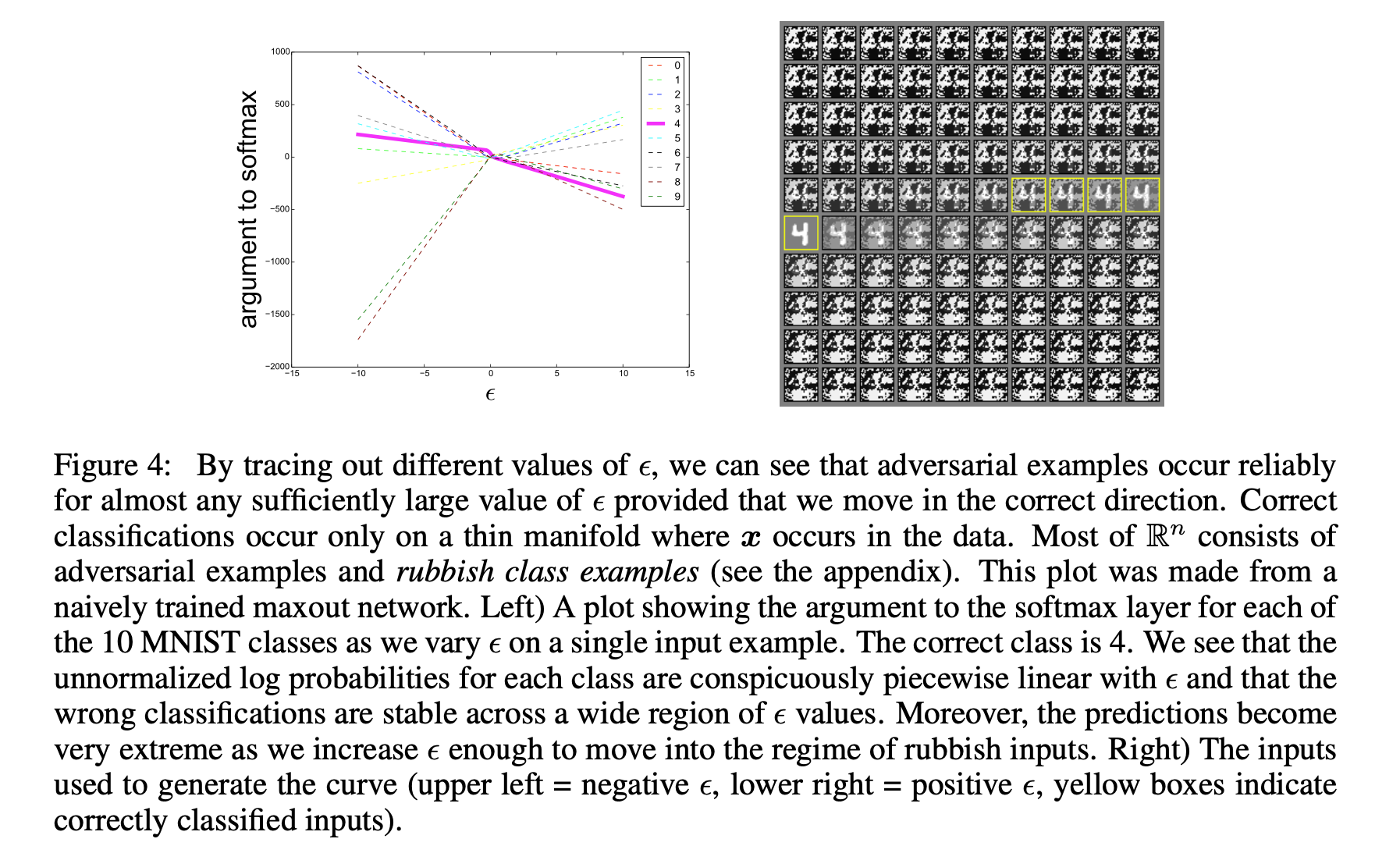
下左图，纵轴是没有经过softmax的概率值，可以见到在同一个方向上，随着$\epsilon$变化，不同类别结果的变化情况。只有在很小的一段里能被识别正确，只要方向正确，步长够大，对抗性样本攻击就会攻击成功。实验证明，以$\epsilon$ 为自变量，对抗样本呈抱团出现。

image-20201030144152704

conclusions

Here is the list of conclusions from the paper which is a superb summary of the paper:

  • Adversarial examples can be explained as a property of high-dimensional dot products.
  • They are a result of models being too linear, rather than too nonlinear.
  • The generalization of adversarial examples across different models can be explained as a result of adversarial perturbations being highly aligned with the weight vectors of a model, and different models learning similar functions when trained to perform the same task.
  • The direction of perturbation, rather than the specific point in space, matters most. Space is not full of pockets of adversarial examples that finely tile the reals like the rational numbers.
  • Because it is the direction that matters most, adversarial perturbations generalize across different clean examples.
  • We have introduced a family of fast methods for generating adversarial examples.
  • We have demonstrated that adversarial training can result in regularization; even further regularization than dropout.
  • We have run control experiments that failed to reproduce this effect with simpler but less efficient regularizers including L1 weight decay and adding noise.
  • Models that are easy to optimize are easy to perturb.
  • Linear models lack the capacity to resist adversarial perturbation; only structures with a hidden layer (where the universal approximator theorem applies) should be trained to resist adversarial perturbation.
  • RBF networks are resistant to adversarial examples.
  • Models trained to model the input distribution are not resistant to adversarial examples.
  • Ensembles are not resistant to adversarial examples.
  • Rubbish class examples are ubiquitous and easily generated.
  • Shallow linear models are not resistant to rubbish class examples
  • RBF networks are resistant to rubbish class examples.

  1. Szegedy, Christian, Zaremba, Wojciech, Sutskever, Ilya, Bruna, Joan, Erhan, Dumitru, Goodfellow, Ian J., and Fergus, Rob. Intriguing properties of neural networks. ICLR, abs/1312.6199, 2014b. URL http: //arxiv.org/abs/1312.6199. ↩ ↩2 ↩3