进化策略是一种模仿生物进化原理提出的参数优化方法。生物的进化总是朝着适于生存的方向发展,而把不适者淘汰。进化策略的核心就是在原样本的基础上生成一堆符合某种分布的随机噪声,生成一堆新样本,再计算出这堆新样本的得分(或者说损失),得分高的保留,得分差的淘汰,经过迭代最后能够找到局部最优解。这样就不用对损失函数求梯度,但也能得到梯度下降的大致方向。
进化策略类的算法分为遗传算法(GA)、协方差矩阵自适应演化策略(CMA-ES)、自然进化策略(NES)、OpenAI的进化策略等。本文结合自己的理解对以上集中主流的进化策略算法所简要的探讨,主要参考“论智”的文章。
进化策略的思想的其实很好理解,简单暴力,比梯度下降算法更直观,直观到不需要解释,看图就行了。但是,不得不说这个算法让我感到恍然大悟,从梯度下降的固定框架中解放出来。
自然梯度,通过求出两点函数值之差,用这个差值去估计真实的梯度,差值越大梯度越大。相对于梯度,两者更像是数值解和解析解的关系。
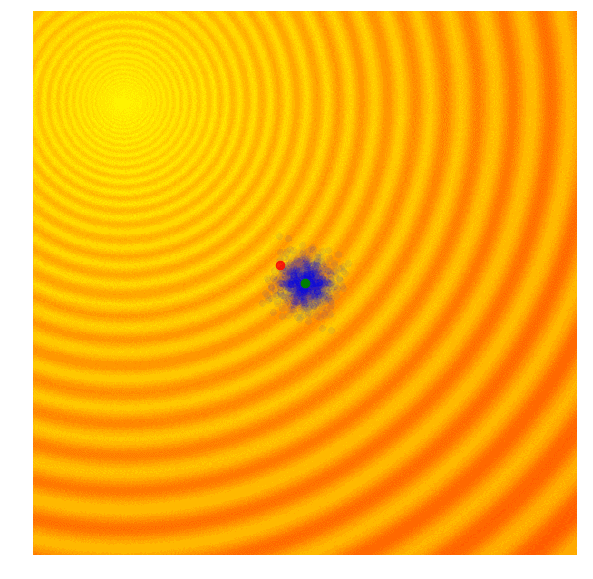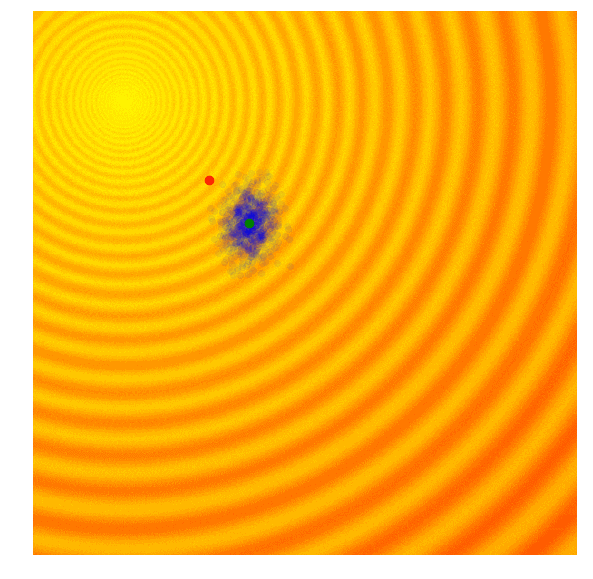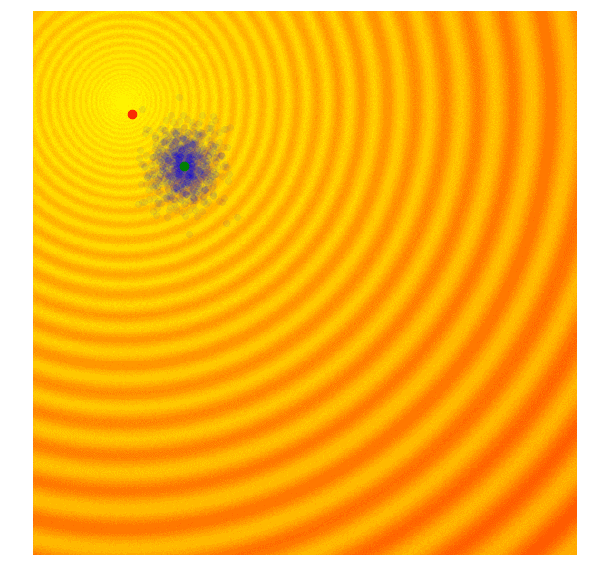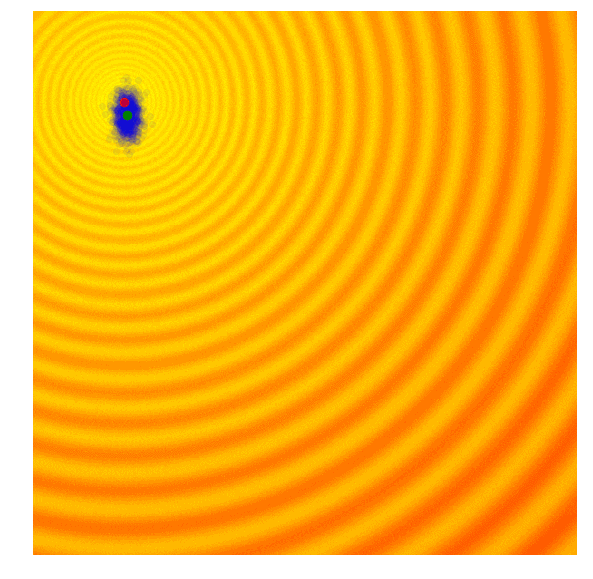
演化策略简单示例
遗传算法(GA)
目的:通过产生固定分布的扰动找到参数的局部最优解
地位:遗传算法是其中历史比较悠久的黑盒优化算法之一,具有很多迭代版本。追本溯源,探讨最根本也是简单的一种。
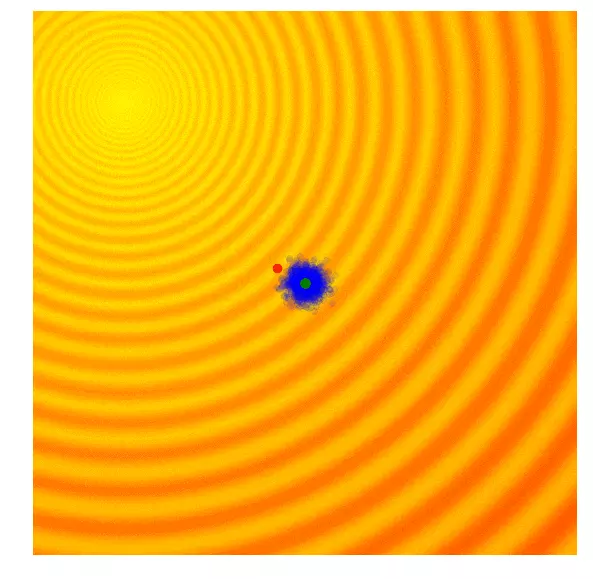
具体实现:只保留当前这一代中一定比例,如前10%的最优解,然后舍去剩下的90%。在下一代,算法从上一代遗留下来的解中随机选择一对父母,并重组它们的参数形成一个新个体。这个新解继承父母x、y参数的概率各占50%,因此带有固定标准差$\sigma$的高斯噪声也会随着重组过程进入每个新的解。遗传算法通过跟踪不同解的参数来重建下一代,虽然一定程度上有利于解的多样性但在具体实践中,这种筛选最优解的做法也会面临最后结果收束到局部最优值的问题。
演示:
协方差矩阵自适应演化策略(CMA-ES)
目的:通过自由化的策略,解决GA随机扰动的方差固定的问题。进化策略是遗传算法的缺点在于设定的标准差是固定的。有时候,我们想要加大步长,上调标准差;有时候,我们认为算法已经接近了最佳值,希望能微调一下解,下调标准差。
地位:这个算法是现在最流行的无梯度优化算法之一,而且广受研究人员和数据科学从业者欢迎。
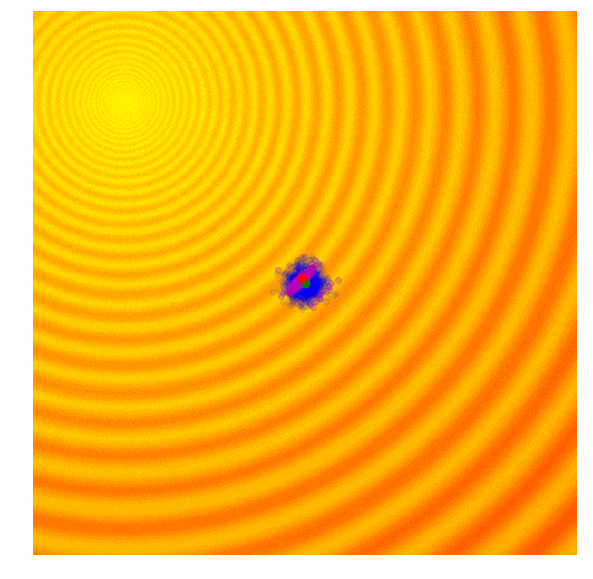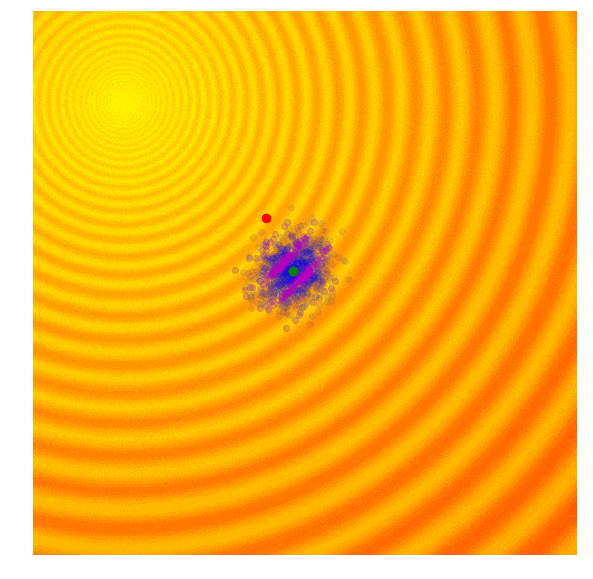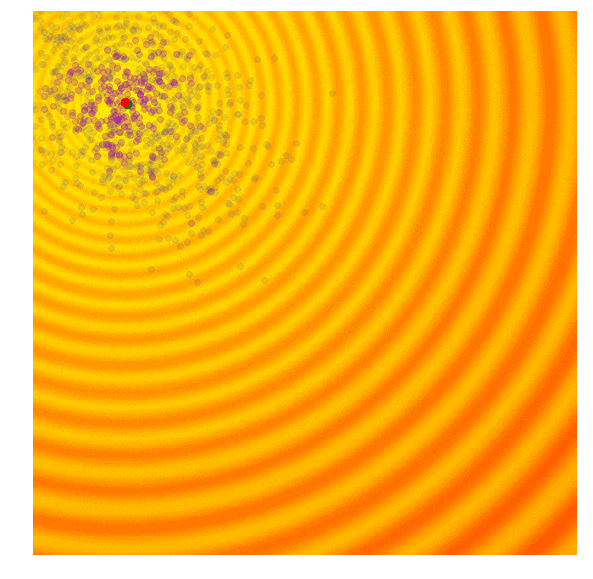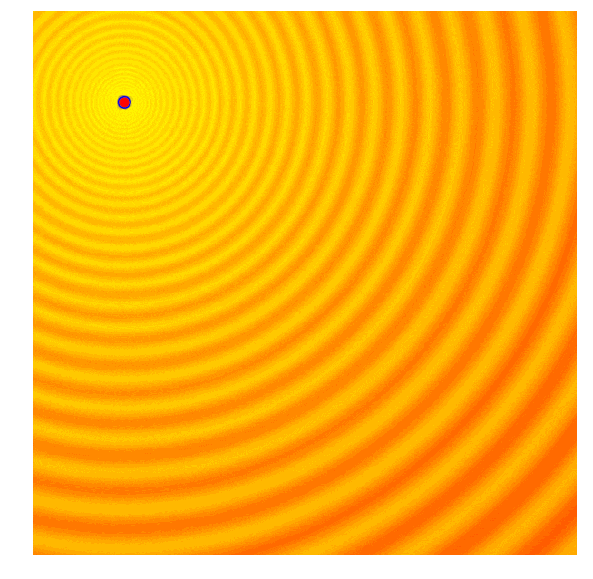
具体实现:在GA的基础上,CMA—ES在每一次迭代的过程中,判断均值与最优样本间的距离来更新下一轮扰动的均值$\mu$和方差$\sigma$。迭代方法如下:
$$
\begin{align}
\mu_x^{(g+1)}&=\frac{1}{N{best}}\sum_{i=1}^{N_{best}}x_i \\
\mu_y^{(g+1)}&=\frac{1}{N{best}}\sum_{i=1}^{N_{best}}y_i \\\
\sigma_{x,(g+1)}^2&=\frac{1}{N_{best}}\sum_{i=1}^{N_{best}}(x_i-\mu_x^{(g)})^2 \\\
\sigma_{y,(g+1)}^2&=\frac{1}{N_{best}}\sum_{i=1}^{N_{best}}(y_i-\mu_y^{(g)})^2 \\
\sigma_{xy,(g+1)}^2&=\frac{1}{N_{best}}\sum_{i=1}^{N_{best}}(y_i-\mu_y^{(g)})(x_i-\mu_x^{(g)})
\end{align}
$$
缺点:性能,计算太慢,适合用于1000个参数以下的搜索空间
演示:

自然化策略(NES)
目的:前面的算法放弃了大部分的分靠后的成员的信息。NES利用了种群中所有成员的信息,无论好坏,它们都可以被用来估计一个梯度信号,并使整个种群在进化到下一代时能朝着更好的方向前进。思路是使得候选解的适应值的期望最大化,如果期望足够好,那么最优候选解应该更好。
实现:
$$
\begin{align}
J(\theta)=E_\theta[F(z)]&=\int F(z)\pi(z,\theta)dz\\
\nabla \theta J(\theta)&=E\theta[F(z)\nabla_\theta \log\pi(z,\theta)] \\
\nabla \theta J(\theta)&\approx \frac{1}{N}\sum^N{i=1}F(z^i)\nabla_\theta\log(z^i,\theta) \\
\end{align}
$$
对多变量高斯分布,$\theta$是$\mu$和$\sigma$的向量,所有解可以从$z_j\sim N(u_j,\sigma_j)$,对$\nabla_\theta\log(z^i,\theta) $的求导公式为:
$$
\begin{align}
\nabla_{\mu_j}\log N(z^i \mu,\sigma)&=\frac{z_j^i-\mu_j}{\sigma_j} \
\nabla_{\sigma_j}\log N(z^i,\mu,\sigma)&=\frac{(z^i_j-\mu_j)^2-\sigma_j^2}{\sigma_j^3}
\end{align}
$$
演示: